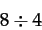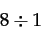Research that fails to impact practice is a problem in any arena, and education is no exception. Teachers have many reasons for not implementing practices based on research. Too often research is unknown to teachers, locked away in journals that teachers and schools cannot afford. Beyond the cost of access, much of the best research is generally written for higher academic audiences and not easily digested by a busy and distracted practicing teacher. Transforming research into improved practice takes time, effort and patience, and is made easier in a professional community who share ideas and experiences. Teachers are constantly improving their practice, but too often the improvements are driven by personal failures or anecdotal evidence, not the quality results of dedicated educational researchers. This is a crippling inefficiency in the field of education, one that is largely self-imposed and tied to traditional practices held in place by the inertia of our experience.
Research strongly suggests that teachers could improve student learning by using formative assessment. Chapter tests and final exams are summative: they summarize the knowledge and skills a student has acquired, and are generally assigned a fixed grade. In fact, any assignment or task assigned a fixed and lasting grade can be considered summative, at least in part. Formative assessment, in contrast, focuses on improvement rather than final measurement. Teachers use formative assessment to adapt their teaching, and students, equal partners in the process, use feedback and self-monitoring to improve their knowledge and skills.
For any classroom teacher, the concept of formative assessment should be comprehensible and implementation should not be impeded by any significant obstacles. So why don't more teachers practice proper formative assessment? I suggest two simple reasons, reasons that could be eliminated by improved understanding between teachers, administrators, teachers, and parents.
Reason 1: Teachers think they're already doing formative assessment. My early understanding of summative versus formative assessment came from my curriculum director, who simply defined the two this way: "Summative assessments are tests and quizzes you grade, and formative assessments are anything you use to guide your instruction. You are already doing formative assessment all the time." These definitions were vague and incomplete, but not necessarily incorrect. The real problem was the message that we were "already doing formative assessment." Why then should we, a room full of teachers feeling burdened yet open to new ideas, seek to improve our practice of something we were apparently already doing? Just as with students, there is danger in false praise. Even worse, I knew my questioning techniques in whole-class activities were lacking. Had I been properly introduced to formative assessment, I may have improved my questioning practices and sought better ways to assess student understanding. I shouldn't have been led to think I was doing something well when in reality, I wasn't, or denied access to information that would have helped me improve.
Reason 2: Teachers are pressured to assess performance with grades. Grading practices can influence assessment practices, and pressure to assign grades for all classroom activity can inhibit the use of true formative assessment. In a world of 24/7 access to online gradebooks, parents and students expect to see near real-time measures of progress and achievement on their computer screens. To expect the full benefits of formative assessment, students must invest themselves in the improvement process as much as teachers. Once a teacher assigns a grade to a task, the message received by the student and parent is of summation – the task is complete, learning has been measured, and it's time to move on to the next task. The teacher might not want to send this message, but what's important is the message received by the student, not what was intended by the teacher. The sophisticated give-and-take of formative assessment is best recorded and measured outside the simple percentages and averages calculated by our technically limited gradebooks.
Formative assessment is understandable and practical, but inhibited by false assumptions. Administrators falsely assume teachers already know and use it, and teachers falsely assume students are willing and able to translate a summative grade into formative feedback. Fortunately, both of these obstacles can be overcome through better a understanding of formative assessment, improved communication, and a commitment to collaboration. Teachers, students, and parents alike should welcome an increased focus on improvement, instead of the summative and often harsh dependence on grades and percentages. Summative assessments and grades might be more familiar, but that doesn't make them easier or more beneficial.
Dividing by Fractions
In his recent post "Math is a dangerous subject to teach," Joe Bower discusses the ability to learn the procedures of math without understanding the conceptual foundations. As an example, Joe humbly admits that he has "absolutely no idea why" (emphasis his) dividing by a fraction is replaced by multiplying by the fraction's reciprocal. He can get the answer right without proper understanding, and therein lies the danger.
One of the things I've enjoyed most about teaching is finding new and deeper ways of understanding so-called "simple" math that I thought I had already mastered. Most of my mathematical upbringing focused more on procedure than understanding, so I occasionally find myself in the same position as Joe. Using Joe's post as inspiration, I've given more thought to dividing by fractions and finally have a model and a description that I hope explains what's really happening when you divide by a fraction.
First, let's look at a simple fraction:
The top number, the numerator, simply counts "how many." The bottom number, the denominator, tells us "how big." We read this fraction properly as "two-thirds," and usually think of that as two objects, each one-third the size of the whole (however big that is).
Now let's look at division. Some students are led astray with early beliefs that "multiplying makes bigger" and "division makes smaller." That kind of misguided number sense can be frighteningly persistent. Multiplication is better thought of as a "scaling" operation, and division can be thought of as a "grouping" operation. To see what I mean, let me explain using whole numbers:
The model I imagine for this problem looks like this:
Using the "grouping" concept of division, I've made four groups. Because each group contains two, the answer is two. No surprise. Let's try another:
The model:
I've made two groups. Because each group contains four, the answer is four. Still no surprises. Let's try one more with whole numbers:
The model:
I've made one group, which is as trivial as it gets. Because the group contains eight, the answer is eight. Now that we've established the pattern with a "grouping" definition, it should be easy to see why you can't divide by zero. I can't possibly make zero groups and still have the eight squares.
Okay, now let's try an easy division problem with fractions:
Remember, the numerator tells us "how many" and the denominator tells us "how big." The model:
It's still one group (how many), but a group of halves (how big). If you count objects, you get the answer: sixteen. But we haven't added or taken away anything -- the eight is still there. Got it? Let's try another:
The model:
Eight divided by two thirds, translated into "grouping-speak," is "eight grouped into two groups of thirds." Because each group contains twelve, the answer is twelve, even though you can still imagine the original eight.
So is this the same as multiplying by the reciprocal? Breaking the wholes into thirds gave us three times as many pieces (24, same as 8 times 3), and grouping into two groups gave us half of the pieces in each group (12, same as 24 divided by 2). More concisely, we multiplied 8 by 3 and divided by two. So doesn't that mean dividing by two thirds is the same as multiplying by three halves? Not exactly. We get the same answer, but for a different reason. To me, the model for eight times three halves would mean scaling eight to be three times bigger (24), then scaled back down to half of that (12). It's a different picture, even if we still get the same answer.
You can choose to accept this as a complication or a convenience; either way, I hope you have a better understanding of dividing by fractions. As always, feel free to offer criticisms in the comments below. (There has to be many a sixth grade teacher who could teach me a thing or two about this topic!)
Update 4/18/2010: Gary Davis co-authored a great guide on the division of fractions. It provides more strategies, more examples, and more detail than my post did. Thanks for sharing, Gary!
One of the things I've enjoyed most about teaching is finding new and deeper ways of understanding so-called "simple" math that I thought I had already mastered. Most of my mathematical upbringing focused more on procedure than understanding, so I occasionally find myself in the same position as Joe. Using Joe's post as inspiration, I've given more thought to dividing by fractions and finally have a model and a description that I hope explains what's really happening when you divide by a fraction.
First, let's look at a simple fraction:
The top number, the numerator, simply counts "how many." The bottom number, the denominator, tells us "how big." We read this fraction properly as "two-thirds," and usually think of that as two objects, each one-third the size of the whole (however big that is).
Now let's look at division. Some students are led astray with early beliefs that "multiplying makes bigger" and "division makes smaller." That kind of misguided number sense can be frighteningly persistent. Multiplication is better thought of as a "scaling" operation, and division can be thought of as a "grouping" operation. To see what I mean, let me explain using whole numbers:
Okay, now let's try an easy division problem with fractions:
So is this the same as multiplying by the reciprocal? Breaking the wholes into thirds gave us three times as many pieces (24, same as 8 times 3), and grouping into two groups gave us half of the pieces in each group (12, same as 24 divided by 2). More concisely, we multiplied 8 by 3 and divided by two. So doesn't that mean dividing by two thirds is the same as multiplying by three halves? Not exactly. We get the same answer, but for a different reason. To me, the model for eight times three halves would mean scaling eight to be three times bigger (24), then scaled back down to half of that (12). It's a different picture, even if we still get the same answer.
You can choose to accept this as a complication or a convenience; either way, I hope you have a better understanding of dividing by fractions. As always, feel free to offer criticisms in the comments below. (There has to be many a sixth grade teacher who could teach me a thing or two about this topic!)
Update 4/18/2010: Gary Davis co-authored a great guide on the division of fractions. It provides more strategies, more examples, and more detail than my post did. Thanks for sharing, Gary!
Peeping Tom: Finding Windows in the Ivory Tower
Today on Twitter, Tom Whitby posted:
I understand the intent of Tom's post: we have too many teachers who have become detached from some of the "big thinkers" in education. It's easy for a teacher, with all the pressures and responsibilities, to become isolated in their classroom with their students. Fortunately, it's easier than ever to traverse the branches of the internet and find leaders in education online, as well as other teachers who want to share, discuss, and debate big ideas in education.
While I'm sure Tom didn't intend for his list to be all-inclusive, all the names listed have something in common: none of those people are current professors of education. I'm not saying that professors have cornered the market of good ideas, but rarely do I see them mentioned on Twitter or elsewhere outside the ivory towers of academia. (Not suprisingly, several professors who are breaking down this wall are professors of educational technology, such as Alec Couros and Scott McLeod.) Trust me: ed school professors care just as deeply about students, schools, and the improvement of our educational system as anyone, and many have wonderfully big thoughts and ideas. In addition, they have a scholarly duty to promote ideas that have been tested and shown to have positive effects, not just ideas that sound like good ideas.
This might not be the place for a lame sports analogy, but I'm thinking of it this way. I love baseball, and I could happily spend hours listening to Bob Costas and Peter Gammons describe the nuances of the game. But if my job is to walk up to the plate and hit a major league fastball, do I want Costas or Gammons as my hitting coach? No! Give me Joe Varva or Rudy Jaramillo. Never heard of them, you say? Well, they're both major league hitting coaches, for the Twins and Cubs, respectively. Costas or Gammons could probably help me get a swing that looks like Joe Mauer's, but I'd need Varva or Jaramillo to help me develop my best swing, not one modeled after somebody else's. And neither Varva or Jaramillo themselves played in the majors. They know what they're doing because they tirelessly treat their jobs as a science. Alfie Kohn isn't Joe Varva. He's Peter Gammons -- an intelligent and thoughtful commentator who is making positive contributions to his profession and our enjoyment, but not necessarily a scientist.
So while you're asking your colleagues about Kohn, Marzano, and Sir Ken, try asking them if they have heard of Linda Darling-Hammond, Deborah Ball, Michael Apple, Truus Dekker, Alan Schoenfeld, or Lorrie Shepard. Don't know them? You should, but if you don't, don't be too hard on yourself. I was disappointed to the see that the list of Race to the Top scorers was heavily populated with educational consultants, institute founders, foundation advocates, and others who might profit from the results, instead of more ed school researchers. So maybe Arne Duncan doesn't know many of the names on my list, either. But it's not all his fault, and not all your fault, either. Our system of higher education and scholarly publishing is holding up those ivory walls, walls that work both ways. Stick to Alfie Kohn and let the wall crumble, or read Linda Darling-Hammond and try to knock it down.
I understand the intent of Tom's post: we have too many teachers who have become detached from some of the "big thinkers" in education. It's easy for a teacher, with all the pressures and responsibilities, to become isolated in their classroom with their students. Fortunately, it's easier than ever to traverse the branches of the internet and find leaders in education online, as well as other teachers who want to share, discuss, and debate big ideas in education.
While I'm sure Tom didn't intend for his list to be all-inclusive, all the names listed have something in common: none of those people are current professors of education. I'm not saying that professors have cornered the market of good ideas, but rarely do I see them mentioned on Twitter or elsewhere outside the ivory towers of academia. (Not suprisingly, several professors who are breaking down this wall are professors of educational technology, such as Alec Couros and Scott McLeod.) Trust me: ed school professors care just as deeply about students, schools, and the improvement of our educational system as anyone, and many have wonderfully big thoughts and ideas. In addition, they have a scholarly duty to promote ideas that have been tested and shown to have positive effects, not just ideas that sound like good ideas.
This might not be the place for a lame sports analogy, but I'm thinking of it this way. I love baseball, and I could happily spend hours listening to Bob Costas and Peter Gammons describe the nuances of the game. But if my job is to walk up to the plate and hit a major league fastball, do I want Costas or Gammons as my hitting coach? No! Give me Joe Varva or Rudy Jaramillo. Never heard of them, you say? Well, they're both major league hitting coaches, for the Twins and Cubs, respectively. Costas or Gammons could probably help me get a swing that looks like Joe Mauer's, but I'd need Varva or Jaramillo to help me develop my best swing, not one modeled after somebody else's. And neither Varva or Jaramillo themselves played in the majors. They know what they're doing because they tirelessly treat their jobs as a science. Alfie Kohn isn't Joe Varva. He's Peter Gammons -- an intelligent and thoughtful commentator who is making positive contributions to his profession and our enjoyment, but not necessarily a scientist.
So while you're asking your colleagues about Kohn, Marzano, and Sir Ken, try asking them if they have heard of Linda Darling-Hammond, Deborah Ball, Michael Apple, Truus Dekker, Alan Schoenfeld, or Lorrie Shepard. Don't know them? You should, but if you don't, don't be too hard on yourself. I was disappointed to the see that the list of Race to the Top scorers was heavily populated with educational consultants, institute founders, foundation advocates, and others who might profit from the results, instead of more ed school researchers. So maybe Arne Duncan doesn't know many of the names on my list, either. But it's not all his fault, and not all your fault, either. Our system of higher education and scholarly publishing is holding up those ivory walls, walls that work both ways. Stick to Alfie Kohn and let the wall crumble, or read Linda Darling-Hammond and try to knock it down.
Survey: Teaching to the Test
Colorado math teachers: I need your input! I have heard many teachers use the phrase "teaching to the test" and I want to know two things:
Many thanks for your cooperation, and I'll be sure to let everyone know the survey results and how they factor into my research. If any of you submit perfect rankings, I believe you deserve some recognition. I'd offer cash prizes, but that's not exactly in my budget. Sorry!
- What does "teaching to the test" mean to you?
- How well do you know the math CSAP test? What is assessed most? And least?
- 3rd Grade Math CSAP
- 4th Grade Math CSAP
- 5th Grade Math CSAP
- 6th Grade Math CSAP
- 7th Grade Math CSAP
- 8th Grade Math CSAP
- 9th Grade Math CSAP
- 10th Grade Math CSAP
Many thanks for your cooperation, and I'll be sure to let everyone know the survey results and how they factor into my research. If any of you submit perfect rankings, I believe you deserve some recognition. I'd offer cash prizes, but that's not exactly in my budget. Sorry!
Conference on World Affairs 2010: Saving the Nation With Math and Science
Tuesday 2:00 Panel, East Ballroom UMC, CU-Boulder
Panelists: Ruth Oratz, Kirsten Sanford (@drkiki), and Erika B. Wagner
(All of the below is paraphrased to the best of my ability, and not necessarily a transcription!)
Dr. Kiki: There is a myth that science is on the way out in this country, that somehow as a nation we've fallen way behind. While there is always room to improve, it's good to focus on what is right with science in the US. Our colleges and universities hold 17 of the top 20 positions for science research worldwide, and people from all over the world come here to study. The public is thankful for science and believes it has done them more good than harm. However, we aren't always very good at communicating what's good and right about science, and that limits both participation and advancement.
Erika B. Wagner: Science has helped our society in countless ways, yet our youth don't rank highly on international assessments and our science workforce, such as our NASA engineers, are approaching retirement with fewer young engineers to replace them. Can we use STEM education to excite the public? We must recognize the frontiers that have been opened by our current levels of math and science, and energize ourselves around new challenges that we have only begun to realize.
Ruth Oratz: I'm thinking literally about using math and science to save us from poor health and diseases such as cancer. Cancer rates worldwide are escalating rapidly, and 30 years of research have helped us better understand cancer and develop new treatments. What we're seeing now is a cooperation of doctors, engineers, mathematicians and statisticians, and other scientists who are unified in their fight against cancer. Unfortunately, the resources to do our best research aren't there. The National Cancer Institute spends a large part of their budget on sustaining older projects, leaving less for new cutting-edge research.
Erika B. Wagner: We need people to take a new perspective on science education. When I used to come home from school, my mother didn't ask me, "Did you learn anything new today?" Instead, she'd ask, "Did you ask any good questions today?" Our kids need to feel empowered to ask good questions.
Q&A:
Q: My question is about motivation. I'm old enough to remember Sputnik, and my friends and I went from wanting to be Buddy Holly at the beginning of the week to wanting to be engineers by the end of the week. What can ignite that passion for science to a new generation?
A: Kiki: I think the internet is broadening people's horizons to science in interactive ways that is generating motivation to study science.
A: Oratz: Social networks of participants is helping science in significant ways, even if the participants are participating in passive ways. People want to help -- even if they aren't scientists.
Q: Do you think having people with math and science degrees, even advanced degrees, is important to teaching math and science and motivate learning in their students?
A: Kiki: Not for the motivation part, but the knowledge is important. We have to change the perception of what it means to be a scientist, that it's more than just working in a lab. Perhaps we could consider lowering the bar to get more people into being science and math teachers, but structure requirements so they develop their expertise over the course of their career.
Q: How do we get science into the public narrative, and how do we restructure our funding to better focus on science?
A: Oratz: Look at what we're up against - we have countless TV channels dedicated to entertainment, but very few Discovery networks. Also, there are still some very "ivory tower" bureaucracies that funnel money to non-progressive efforts and institutions.
A: Kiki: There are some efforts, such as the show "The Big Bang Thoery" and efforts to make science fiction more scientifically accurate. Still, we need a better narrative.
Q: In math and science postsecondary ed, how many students are American vs. how many come from other countries?
A: Kiki: I'm not aware of the numbers, but we have the best institutions in the world, so we attract the best students from around the world. Some of those students stay, some don't, and some can't.
A: Wagner: We need some reform of our work visa policies to help top talent stay in the country.
Summary: The Q&A continued with numerous questions about improving math and science education. Some were anecdotal about particular course requirements or tests in particular schools or districts, but that's the dialogue you expect in open forums like the Conference on World Affairs. Still, there were plenty of good questions and, as can be expected, it's hard to come up with 2-minute answers that will solve our educational problems in math and science. I appreciate Ruth Oratz's forthrightness about money being an issue, and I believe she successfully argued it's targeted funding we need, not just more dollars spread thin across our educational and research systems.
Panelists: Ruth Oratz, Kirsten Sanford (@drkiki), and Erika B. Wagner
(All of the below is paraphrased to the best of my ability, and not necessarily a transcription!)
Dr. Kiki: There is a myth that science is on the way out in this country, that somehow as a nation we've fallen way behind. While there is always room to improve, it's good to focus on what is right with science in the US. Our colleges and universities hold 17 of the top 20 positions for science research worldwide, and people from all over the world come here to study. The public is thankful for science and believes it has done them more good than harm. However, we aren't always very good at communicating what's good and right about science, and that limits both participation and advancement.
Erika B. Wagner: Science has helped our society in countless ways, yet our youth don't rank highly on international assessments and our science workforce, such as our NASA engineers, are approaching retirement with fewer young engineers to replace them. Can we use STEM education to excite the public? We must recognize the frontiers that have been opened by our current levels of math and science, and energize ourselves around new challenges that we have only begun to realize.
Ruth Oratz: I'm thinking literally about using math and science to save us from poor health and diseases such as cancer. Cancer rates worldwide are escalating rapidly, and 30 years of research have helped us better understand cancer and develop new treatments. What we're seeing now is a cooperation of doctors, engineers, mathematicians and statisticians, and other scientists who are unified in their fight against cancer. Unfortunately, the resources to do our best research aren't there. The National Cancer Institute spends a large part of their budget on sustaining older projects, leaving less for new cutting-edge research.
Erika B. Wagner: We need people to take a new perspective on science education. When I used to come home from school, my mother didn't ask me, "Did you learn anything new today?" Instead, she'd ask, "Did you ask any good questions today?" Our kids need to feel empowered to ask good questions.
Q&A:
Q: My question is about motivation. I'm old enough to remember Sputnik, and my friends and I went from wanting to be Buddy Holly at the beginning of the week to wanting to be engineers by the end of the week. What can ignite that passion for science to a new generation?
A: Kiki: I think the internet is broadening people's horizons to science in interactive ways that is generating motivation to study science.
A: Oratz: Social networks of participants is helping science in significant ways, even if the participants are participating in passive ways. People want to help -- even if they aren't scientists.
Q: Do you think having people with math and science degrees, even advanced degrees, is important to teaching math and science and motivate learning in their students?
A: Kiki: Not for the motivation part, but the knowledge is important. We have to change the perception of what it means to be a scientist, that it's more than just working in a lab. Perhaps we could consider lowering the bar to get more people into being science and math teachers, but structure requirements so they develop their expertise over the course of their career.
Q: How do we get science into the public narrative, and how do we restructure our funding to better focus on science?
A: Oratz: Look at what we're up against - we have countless TV channels dedicated to entertainment, but very few Discovery networks. Also, there are still some very "ivory tower" bureaucracies that funnel money to non-progressive efforts and institutions.
A: Kiki: There are some efforts, such as the show "The Big Bang Thoery" and efforts to make science fiction more scientifically accurate. Still, we need a better narrative.
Q: In math and science postsecondary ed, how many students are American vs. how many come from other countries?
A: Kiki: I'm not aware of the numbers, but we have the best institutions in the world, so we attract the best students from around the world. Some of those students stay, some don't, and some can't.
A: Wagner: We need some reform of our work visa policies to help top talent stay in the country.
Summary: The Q&A continued with numerous questions about improving math and science education. Some were anecdotal about particular course requirements or tests in particular schools or districts, but that's the dialogue you expect in open forums like the Conference on World Affairs. Still, there were plenty of good questions and, as can be expected, it's hard to come up with 2-minute answers that will solve our educational problems in math and science. I appreciate Ruth Oratz's forthrightness about money being an issue, and I believe she successfully argued it's targeted funding we need, not just more dollars spread thin across our educational and research systems.
Subscribe to:
Posts (Atom)