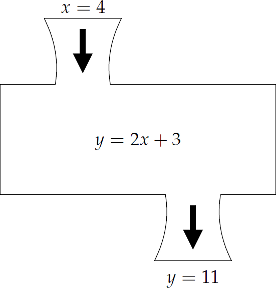
My first experience trying to teach the definition in a non-traditional way was using the "Cola Machine" problem in CPM Algebra (Math 1). The problem, several days into Unit 11, describes the following:
The cola machine at your school offers several types of soda. Your favorite drink, Blast!, has two buttons dedicated to it, while the other drinks (Slurp, Lemon Twister, and Diet Slurp) each have one button.Most textbooks define functions approximately the same way: a relation is a function if there exists no more than one output for each input. Without a context, however, that definition might not carry much meaning, and relying solely on the vertical line test in a graph may not be helpful enough for many students. The soda machine problem, with its emphasis on consistency, gives both teacher and student a very approachable context within which to discuss what a function is and is not.
- Explain how the soda machine is a relation.
- Describe the domain and range of this soda machine.
- While buying a soda, Mr. Hagen pushed the button for Lemon Twister and got a can of Lemon Twister. Later he went back to the same machine but this time pushing the Lemon Twister button got him a can of Blast! Is the machine functioning consistently? Why or why not?
- When Karen pushed the top button for Blast! She received a can of Blast! Her friend, Miguel, decided to be different and pushed the second button for Blast! He, too, received a can of Blast! Is the machine functioning consistently? Why or why not?
- When Loufti pushed a button for Slurp, he received a can of Lemon Twister! Later, Tayeisha also pushed the Slurp button and received a can of Lemon Twister. Still later, Tayeisha noticed that everyone else who pushed the Slurp button received a Lemon Twister. Is the machine functioning consistently? Explain why or why not. (Sallee, et. al., 2002, p. 375)
Early in my teaching career I thought Algebra 1 basically boiled down to two big ideas: solving equations and graphing lines. If students could do those two things, I felt pretty good about them passing my class. Now I see the big ideas of Algebra 1 differently and basically aligned with Colorado's revised standards for high school mathematics. The six expectations listed for Colorado's high school algebra standard can be summarized as follows:
- Functional representations (equations, graphs, and tables)
- Function behavior (qualitative)
- Function transformations (parameters and parent graphs)
- Equivalent expressions, equations, and inequalities
- Solving equations, inequalities, and systems of equations
- Mathematical modeling using functions
I think it's a mistake to delay the explanation and definition of functions until late in Algebra 1 or later. Algebra 1 and younger students can understand the cola machine problem or other, similar contexts. Suppose the class plays an "exchange" game. Student A gives the teacher three triangles in exchange for two squares. What should Student B expect to get in exchange for his three triangles? What exchange would represent a function versus a non-function? For something based more in the real-world, this conversation could be set in the context of currency exchange. Also, a helpful model for learning functions might be function machines, such as:
Function machines are helpful models for learning functions, function composition, inverse functions, and even solving equations. They help stress the input-output relationship in a way that words or equations alone might not. Students will also naturally expect a single output for each input. The real challenge for Algebra 1 or younger students is to present a variety of equations that aren't functions, or else risk having students think that every two-variable equation describes a function.
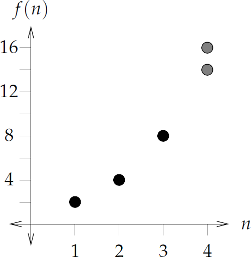
Patterns can also be used to teach functions. If students are given the sequence 2, 4, 8, …, some students are likely to predict 14 as the next term (adding 8 plus 6, the next consecutive even number), while other students might predict 16 (the fourth power of two). Because the fourth term could reasonably be two different values, we can't establish a functional relationship to describe the sequence. This could even be an example worth graphing to discuss the meaning of the vertical line test:
Our calculators also help us distinguish functions from non-functions. If you try to graph a circle on a Texas Instruments graphing calculator, you have to enter two functions: one for the top half of the circle, and one for the bottom half. Therefore, the written forms of the equation of a circle (such as \( x^2 + y^2 = 1\) or \(y= \pm \sqrt{1-x^2} \)) can't be functions. The graphing calculator is also a good tool for discussing the square root function, and why its graph must only be half of a parabola's inverse if we want it to be a function.
There two key obstacles that are likely to remain in a student's way of understanding functions. First, students will continue to focus the vast majority of the time and effort on functions, and there are too few real-world examples of useful non-functions to help distinguish the two. Non-functions are less powerful and less common, but without them we risk having students who casually accept that any equations with an input-output relationship is a function. The second obstacle is notation, and it's not an obstacle we can likely avoid. The change to function notation, such as using \(f(x) = 3x - 2\) instead of \(y = 3x - 2\), is not only difficult to explain as something other than an arbitrary change in symbols, but includes two aspects that are directly contrary to a student's prior knowledge. Now a letter (such as the \(f\) in the preceding example) is no longer a variable, but a name with no numerical value by itself. Function notation also uses parentheses to represent something other than multiplication, adding more work to the already overloaded duties mathematicians place on these two simple arcs. The power of function notation is the preservation of the input (\(x\)) with the output, but it's confusing that the output (\(f(x)\)) reuses the input variable, uses a letter that isn't a variable, and uses symbolism for multiplication of variables that's no longer multiplication. Perhaps a question like this could help students realize the power of the notation:
- If \(y=16\), \(y=49\), and \(y=64\), what might be an equation relating an input, \(x\), to the output, \(y\)?
- If \(f(4)=16\), \(f(7)=49\), and \(f(-8)=64\), what is \(f(x)\)?
- Are the two questions above the same? Which one is easiest to understand? Why?
References
Sallee, T., Kysh, J., Kasimatis, E., & Hoey, B. (2002). College Preparatory Mathematics 1 (Algebra 1). (L. Dietiker, Ed.) (2nd ed., Vols. 1-2, Vol. 2). Sacramento, CA: CPM Educational Program.